Paxos算法的数学归纳法证明

本文是对Paxos算法的证明，如有错误请指正。

预备知识

表面上看，Paxos像是一个Quorum算法再加上二阶段提交(2PC)。但并非是的二者相加。

相关笔记

Quorum算法学习笔记
数学归纳法
使用坐标系分析Paxos算法

证明步骤

Paxos算法需要证明，如果存在已经达成的共识，在节点的任意一个多数派中，ProposalID最大的那个决议必然存有当前共识内容。
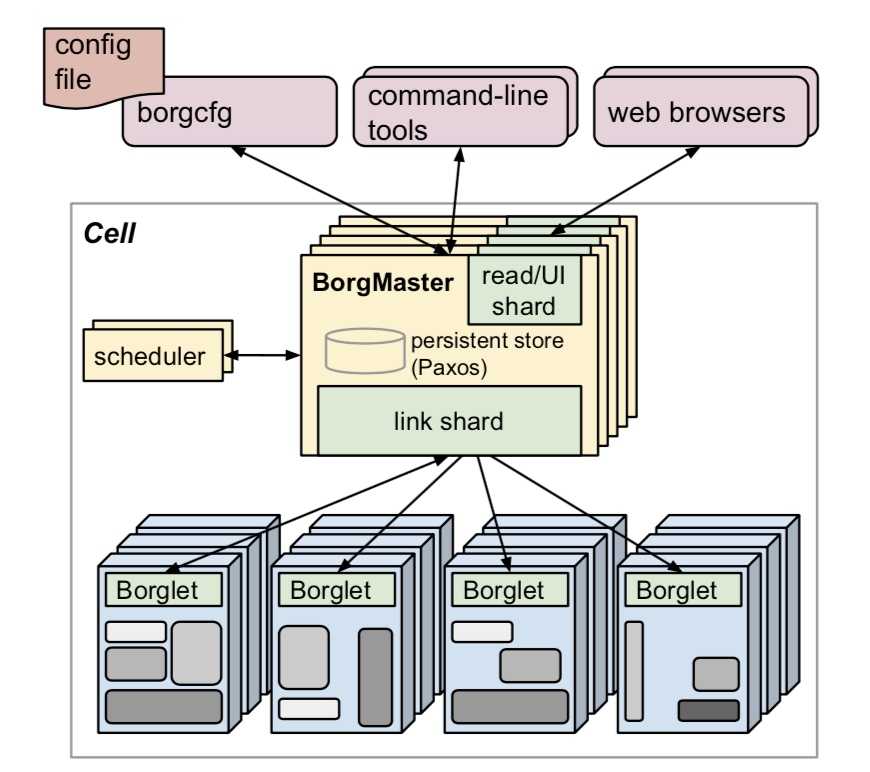
算法流程请参照Paxos算法学习笔记

数学表达

存在已达成的共识是{n0,v0}，在节点的任意一个多数派中，一定存在ProposalID最大的决议{nx,vx}符合nx>=n0 && vx=v0。
为了简便，缩写为命题A。

起始

当只有一个提案并达成共识时。
显然，共识的ProposalID是所有决议中最大的nx=n0 && v=v0。结论成立。

递推

需证明

1. 假设，命题A成立。
2. 可推理出未来无论什么时间点，命题A都会成立。

证明

假设新的提案是为{n1,v1},n1=n0+1,根据Paxos流程:
Preapre阶段
1. Prepare阶段未得到多数派的Promise，流程终止。不会达成新的决议，命题A成立。
2. Prepare执行成功，获得多数派的Promise。此时Proposor需从Promise中获取ProposalID最大的决议。根据命题A的结论，Proposor选择的决议{nx,nx}必然符合nx>=n0 && vx=v0。

Accept阶段
由于提案内容vx=v0，提案为{n1,v0}，在Accept阶段会有两种情况。
1. proposalValue非v0的Acceptor，接受了提案。共识的集合扩大。命题A成立。
2. proposalID小于n1的Acceptor，接受了提案，proposalID变大，proposalValue还是v0。命题A成立。

综上所述，可得出结论命题A成立。
根据命题A可推断出未来达成的所有共识{n,v}必然符合n>=n0 && v==v0。
可得出结论，Paxos算法成立。

总结

1. Prepare达成多数派Promise是非常关键的节点，它将会拦截所有早的提案。
2. Accept阶段，同时会检查Prepare达成的多数派是否还存在，如果不存在，则提案失败。
3. 多数派的存在是为了保证上述关键时间至少有一个节点会产生锁的效果，拦截失败的提案。
4. 一旦形成共识，后续提案必须使用已达成的共识的内容，保证共识不会被改变。