适用场景：对2的幂进行取模。

代码

这是一个来自coolshell的代码
代码本身很简单，就是遍历一个整型数组，每16个值自增1，当遍历到最后一个值，就重头开始。因为要从头开始，所以在遍历的循环中，需要用对数组长度行取模。

int steps = 64 * 1024 * 1024;
// Arbitrary number of steps
int lengthMod = arr.Length - 1;
for (int i = 0; i < steps; i++)
{
    arr[(i * 16) & lengthMod]++;   // (x & lengthMod) is equal to (x % arr.Length)
}

分析

注释中提到 (x & lengthMod) is equal to (x % arr.Length)。
第一次见到这种优化，各种查资料才发现，其实这个有一个条件，即通常只有模去 2^n 才好直接用位运算做,x mod 2^n = x & (2^n-1)。

至于原理，换算成二进制一切都清楚了。

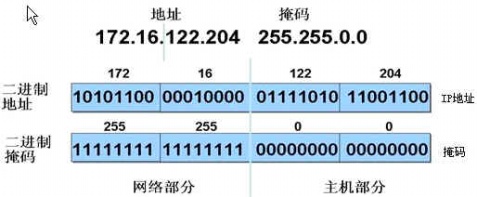
IP地址掩码

类似IP地址，我们可以将其拆解成二进制。

二进制位移

二进制的左右位移，对应的是乘2和除2的操作。

原理

回到上面的代码，我们可以发现，因为除数是2^n，那么它二进制是一个1000..0(n个0)的形式。x在从n位（从右往左数）开始必然是2^n的倍数。取模的话，就是从右往左数n-1位的值。所以，让x^n-1使得那块全变为1，然后进行与运算，就得到模值了。

相对于通常的取模，位运算会更快。这是个不错的优化。